|
Ваше время |
ОФИЦИАЛЬНЫЙ САЙТ КОМПАНИИ DiD Директор: Изаак Д.Д. 
|
Орское время |
|
 |
 |
 |
 |
 |
 |
 |
| СБОРНИК ЗАДАЧ |
|
Представляем Вашему вниманию Сборник Задач По Математике Повышенной Трудности.
Сборник был создан в 1998-м году Изааком Д.Д. и Изааком Д.Ф.
Большую работу редактора провела Бонди И.Л.
Особенность сборника заключается в том, что около трех четвертей задач являются авторскими.
Хотя, эта цифра весьма условна: в любой авторской задаче всё равно какой-то процент идеи является заимствованным.
Некоторые из этих задач были опубликованы в журналах "Квант" и "Математика в Школе".
Сборник содержит не только условия задач, но и решения, однако в html-формате приведены только условия задач.
Настоящий сборник задач по математике предназначен для учащихся 6-11 классов и может служить пособием для школьных учителей в проведении математических олимпиад, а также в проведении факультативных занятий по математике. Сборник состоит из введения и ста задач, разбитых по 20 задач на 5 разделов:
 |
1) 
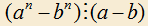для любых натуральных a, b, n. 
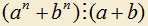для любых натуральных a, b и нечетных n.
2) Площадь эллипса вычисляется по формуле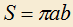
, где a и b — его полуоси.
3) Производные от обратных тригонометрических функций вычисляются по следующим формулам:
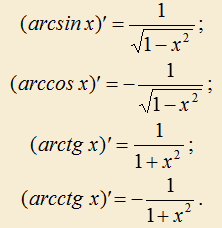
4) Вероятностью p(A) события A называется отношение числа благоприятствующих событию A исходов m к общему числу n всех возможных исходов испытания, образующих группу равновозможных исходов, любые два из которых не могут произойти одновременно, то есть
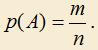
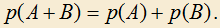
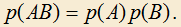
5) Пусть P(n) — некоторое утверждение, где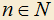
. Тогда согласно принципу математической индукции это утверждение будет верно для всех натуральных n, если
a) P(1) — истинно;
b) Из предположения истинности P(k) следует истинность P(k+1).
6) Если в треугольнике ABC проведена биссектриса BD, то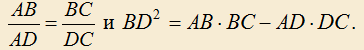
7) Геометрическим местом точек, отношение расстояний которых до концов данного отрезка равно константе, отличной от единицы, является окружность.
8) Если H — ортоцентр треугольника ABC (точка пересечения его высот), то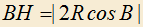
, где R — радиус описанной окружности.
9) Если J — точка пересечения биссектрис треугольника ABC, и M — середина дуги AC, то MA=MC=MJ.
10) Если O — точка Брокара в треугольнике ABC, то есть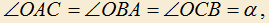
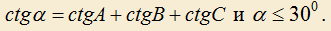
11) Если в остроугольном треугольнике ABC проведены высоты AA1, BB1, CC1, H — точка их пересечения, то H — точка пересечения биссектрис в треугольнике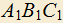
.
12) Если O — центр окружности, описанной около треугольника ABC, то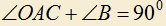
.
13) Если в треугольниках ABC и,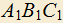 
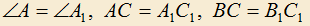, и 
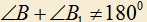, то треугольники равны.
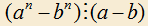для любых натуральных a, b, n. 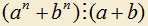для любых натуральных a, b и нечетных n.
2) Площадь эллипса вычисляется по формуле
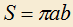, где a и b — его полуоси.
3) Производные от обратных тригонометрических функций вычисляются по следующим формулам:
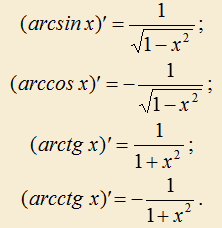
4) Вероятностью p(A) события A называется отношение числа благоприятствующих событию A исходов m к общему числу n всех возможных исходов испытания, образующих группу равновозможных исходов, любые два из которых не могут произойти одновременно, то есть
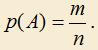
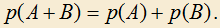
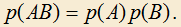
5) Пусть P(n) — некоторое утверждение, где
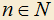. Тогда согласно принципу математической индукции это утверждение будет верно для всех натуральных n, если
a) P(1) — истинно;
b) Из предположения истинности P(k) следует истинность P(k+1).
6) Если в треугольнике ABC проведена биссектриса BD, то
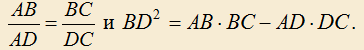
7) Геометрическим местом точек, отношение расстояний которых до концов данного отрезка равно константе, отличной от единицы, является окружность.
8) Если H — ортоцентр треугольника ABC (точка пересечения его высот), то
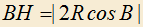, где R — радиус описанной окружности.
9) Если J — точка пересечения биссектрис треугольника ABC, и M — середина дуги AC, то MA=MC=MJ.
10) Если O — точка Брокара в треугольнике ABC, то есть
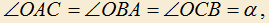
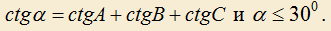
11) Если в остроугольном треугольнике ABC проведены высоты AA1, BB1, CC1, H — точка их пересечения, то H — точка пересечения биссектрис в треугольнике
.
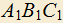12) Если O — центр окружности, описанной около треугольника ABC, то
.
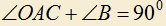13) Если в треугольниках ABC 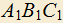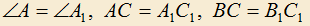и
, , и 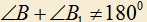, то треугольники равны.
1.1) Расставьте вместо букв необходимые цифры, если известно, что разные буквы обозначают разные цифры:
a)
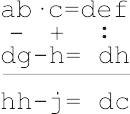
b)
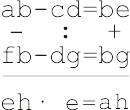
c)
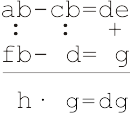
1.2) Расставьте вместо букв необходимые цифры, если известно, что разные буквы обозначают разные цифры:
1.3) В обычном бильярде шары раскладывают треугольником, сторона такого треугольника состоит из четырех шаров, а всего в треугольнике 10 шаров. Сколько шаров будет в треугольнике, сторона которого состоит из N шаров?
1.4) Буквами a, b, c, d обозначены числа 1, 2, 3, 4. Известно, что среди следующих неравенств одно истинно, а три ложных: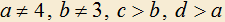
. Определите, какая буква обозначает какое число.
1.5) В шахматном турнире участвовало 5 человек: A, B, C, D и E. Каждый с каждым сыграл по одной партии. Известно, что B и E поделили первое и второе места, у B не было ничьих, у E — две ничьи и два выигрыша, у C — две ничьи и два проигрыша, у A и D не было выигрышей. Выясните, кто с кем как сыграл.
1.6) У шестиклассника 10 предметов. После окончания учебного года выяснилось, что его средний бал 4,6. Сколько у шестиклассника троек, четверок и пятерок, если известно, что в итоговых есть все эти оценки?
1.7) Прямоугольник со сторонами m и n (m и n — целые числа) разбит прямыми, параллельными сторонам на mn клеток. Требуется перебраться из нижней левой клетки в верхнюю правую, побывав в каждой клетке ровно один раз, и перемещаясь только параллельно линиям сетки. При каких m и n это невозможно?
1.8) Какие цифры встречаются на циферблате электронных часов чаще других в течении суток, а какие реже?
1.9) Пусть дан бесконечный лист бумаги в клетку. Узлами будем называть точки пересечения пропечатанных линий. Можно ли через каждый такой узел провести хотя бы по одной прямой так, чтобы она не проходила ни через один из остальных узлов?
1.10) Мне теперь вдвое больше лет, чем было Вам тогда, когда мне было столько, сколько Вам теперь. Когда Вам будет столько, сколько мне теперь, то нам вместе будет 63 года. Сколько лет каждому теперь?
1.11) Петя вскапывает грядку на a минут дольше, чем он это делает вместе с Васей. Вася вскапывает ту же грядку на b минут дольше, чем он это сделал бы вместе с Петей. За сколько минут вскопают ту же грядку Вася и Петя вместе?
1.12) Даны 3 окружности. Если первую вращать вокруг второй без скольжения, то, сделав ровно один оборот вокруг второй окружности, первая совершит некоторое целое количество оборотов n1 вокруг своей оси. Если вторую вращать вокруг третьей без скольжения, то, сделав ровно один оборот вокруг третьей окружности, вторая совершит некоторое целое количество оборотов n2 вокруг своей оси. Если же первую вращать вокруг третьей без скольжения, то, сделав ровно один оборот вокруг третьей окружности, первая совершит ровно 1998 оборотов вокруг своей оси. Найти n1, n2.
1.13) Пусть f(x) — четная функция, то есть
для всех x из множества действительных чисел. Пусть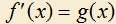 
. Проведем следующие рассуждения:
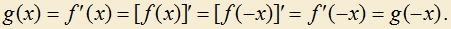
1.14) Из колоды карт выбрано 16 картинок. Достоинства карт следующие: валет, дама, король и туз соответственно — 2, 3, 4 и 11 очков. Все 16 карт поровну розданы четырем игрокам. Сколькими комбинациями можно раздать карты так, чтобы сумма очков у каждого игрока оказалась бы одна и та же? (Карты различной масти, но одинакового достоинства считаются различными.)
1.15) Имеется колода в 36 карт. Достоинства карт следующие: валет, дама, король и туз соответственно — 2, 3, 4 и 11 очков, достоинство остальных карт совпадает с их названием. Двое играют в такую игру: один из них вытягивает из колоды по одной некоторое число карт так, чтобы сумма всех очков по возможности была близка к 21, но оставалась бы меньше 21. Если сумма карт превысила это значение, то говорят, игрок «сгорел», то есть проиграл. Затем второй игрок проделывает ту же процедуру. Выигрывает тот, у кого число набранных очков наиболее близко к 21, но нет перебора. (Упрощенная игра в «Очко».) В одном из конов первый игрок взял из колоды некоторое количество карт и заявил: если я возьму еще одну карту, то шансов на то, что я «сгорю» ровно столько же, сколько на то, что я «не сгорю». Каково возможное количество комбинаций карт у этого игрока? (Карты различной масти, но одинакового достоинства не различаются.)
1.16) Математику P сообщили произведение двух натуральных чисел X и Y, каждое из которых больше 1, а математику S их сумму. Последовал диалог:
a) P1 : — Я не могу назвать числа X и Y.
S1 : — Тогда я их знаю.
Требуется отгадать числа X и Y, если их сумма X+Y=7.
b) P1 : — Я не могу назвать числа X и Y.
S1 : — Я заранее знал, что вы не сможете их назвать.
P2 : — Но тогда я их знаю.
Требуется отгадать числа X и Y, если их произведение XY=18.
c) P1 : — Я не могу назвать числа X и Y.
S1 : — Я заранее знал, что вы не сможете их назвать.
P2 : — Я и после этого не могу назвать числа X и Y.
Требуется отгадать числа X и Y, если их сумма X+Y=11.
1.17) Двое играют в такую игру. В трех клетках записаны числа 1, 2, 3. Начинающий игру должен число в одной клетке заменить целым числом, большим того, которое было записано, но не большим: a) 9, b) 10. Второй игрок делает такой же ход, и так далее. Выигрывает тот, который делает последний ход. Как должен играть первый игрок (начинающий игру), чтобы выиграть при любом ходе второго игрока?
1.18) Найти сумму всех 8! чисел, которые можно получить всевозможными перестановками цифр в числе 12345678.
1.19) a) Двое на счетах играют в такую игру: первый откладывает на счетах любое натуральное число, не большее n, после этого второй добавляет к нему любое натуральное число, не большее n. Затем делает ход первый игрок, и так далее. Выигрывает тот, после хода которого на счетах будет число s,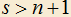
. Как должен играть первый игрок, чтобы обеспечить себе победу? Всегда ли это возможно?
b) Двое на счетах играют в такую игру: первый откладывает на счетах любое натуральное число, не большее n, после этого второй добавляет к нему любое натуральное число, не большее n+1. Затем делает ход первый игрок, и так далее. Выигрывает тот, после хода которого на счетах будет число s,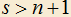. Покажите, что при любой игре первого второй может выиграть игру.
1.20) Восьмикласснику предстоит сдать зачет по математике, на котором ему будет предложено решить 5 задач. Принимать зачет будут две ЭВМ, причем одна из них будет предлагать 3 ответа для каждой задачи, один из которых будет правильный, и эта ЭВМ будет ставить зачет, если ученик решит 3 задачи. Другая будет предлагать два ответа для каждой задачи, один из которых будет правильный, вторая ЭВМ будет ставить зачет, если ученик решит 4 задачи. Какой ЭВМ восьмикласснику выгоднее сдавать зачет? (Выбрать соответствующую ЭВМ нужно до того, как восьмикласснику будут предложены задачи.)
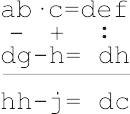
b)
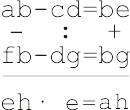
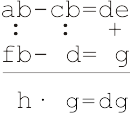
c)1.2) Расставьте вместо букв необходимые цифры, если известно, что разные буквы обозначают разные цифры:
1.3) В обычном бильярде шары раскладывают треугольником, сторона такого треугольника состоит из четырех шаров, а всего в треугольнике 10 шаров. Сколько шаров будет в треугольнике, сторона которого состоит из N шаров?
1.4) Буквами a, b, c, d обозначены числа 1, 2, 3, 4. Известно, что среди следующих неравенств одно истинно, а три ложных:
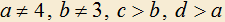. Определите, какая буква обозначает какое число.
1.5) В шахматном турнире участвовало 5 человек: A, B, C, D и E. Каждый с каждым сыграл по одной партии. Известно, что B и E поделили первое и второе места, у B не было ничьих, у E — две ничьи и два выигрыша, у C — две ничьи и два проигрыша, у A и D не было выигрышей. Выясните, кто с кем как сыграл.
1.6) У шестиклассника 10 предметов. После окончания учебного года выяснилось, что его средний бал 4,6. Сколько у шестиклассника троек, четверок и пятерок, если известно, что в итоговых есть все эти оценки?
1.7) Прямоугольник со сторонами m и n (m и n — целые числа) разбит прямыми, параллельными сторонам на mn клеток. Требуется перебраться из нижней левой клетки в верхнюю правую, побывав в каждой клетке ровно один раз, и перемещаясь только параллельно линиям сетки. При каких m и n это невозможно?
1.8) Какие цифры встречаются на циферблате электронных часов чаще других в течении суток, а какие реже?
1.9) Пусть дан бесконечный лист бумаги в клетку. Узлами будем называть точки пересечения пропечатанных линий. Можно ли через каждый такой узел провести хотя бы по одной прямой так, чтобы она не проходила ни через один из остальных узлов?
1.10) Мне теперь вдвое больше лет, чем было Вам тогда, когда мне было столько, сколько Вам теперь. Когда Вам будет столько, сколько мне теперь, то нам вместе будет 63 года. Сколько лет каждому теперь?
1.11) Петя вскапывает грядку на a минут дольше, чем он это делает вместе с Васей. Вася вскапывает ту же грядку на b минут дольше, чем он это сделал бы вместе с Петей. За сколько минут вскопают ту же грядку Вася и Петя вместе?
1.12) Даны 3 окружности. Если первую вращать вокруг второй без скольжения, то, сделав ровно один оборот вокруг второй окружности, первая совершит некоторое целое количество оборотов n1 вокруг своей оси. Если вторую вращать вокруг третьей без скольжения, то, сделав ровно один оборот вокруг третьей окружности, вторая совершит некоторое целое количество оборотов n2 вокруг своей оси. Если же первую вращать вокруг третьей без скольжения, то, сделав ровно один оборот вокруг третьей окружности, первая совершит ровно 1998 оборотов вокруг своей оси. Найти n1, n2.
1.13) Пусть f(x) — четная функция, то есть
для всех x из множества действительных чисел. Пусть 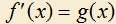. Проведем следующие рассуждения:
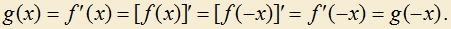
1.14) Из колоды карт выбрано 16 картинок. Достоинства карт следующие: валет, дама, король и туз соответственно — 2, 3, 4 и 11 очков. Все 16 карт поровну розданы четырем игрокам. Сколькими комбинациями можно раздать карты так, чтобы сумма очков у каждого игрока оказалась бы одна и та же? (Карты различной масти, но одинакового достоинства считаются различными.)
1.15) Имеется колода в 36 карт. Достоинства карт следующие: валет, дама, король и туз соответственно — 2, 3, 4 и 11 очков, достоинство остальных карт совпадает с их названием. Двое играют в такую игру: один из них вытягивает из колоды по одной некоторое число карт так, чтобы сумма всех очков по возможности была близка к 21, но оставалась бы меньше 21. Если сумма карт превысила это значение, то говорят, игрок «сгорел», то есть проиграл. Затем второй игрок проделывает ту же процедуру. Выигрывает тот, у кого число набранных очков наиболее близко к 21, но нет перебора. (Упрощенная игра в «Очко».) В одном из конов первый игрок взял из колоды некоторое количество карт и заявил: если я возьму еще одну карту, то шансов на то, что я «сгорю» ровно столько же, сколько на то, что я «не сгорю». Каково возможное количество комбинаций карт у этого игрока? (Карты различной масти, но одинакового достоинства не различаются.)
1.16) Математику P сообщили произведение двух натуральных чисел X и Y, каждое из которых больше 1, а математику S их сумму. Последовал диалог:
a) P1 : — Я не могу назвать числа X и Y.
S1 : — Тогда я их знаю.
Требуется отгадать числа X и Y, если их сумма X+Y=7.
b) P1 : — Я не могу назвать числа X и Y.
S1 : — Я заранее знал, что вы не сможете их назвать.
P2 : — Но тогда я их знаю.
Требуется отгадать числа X и Y, если их произведение XY=18.
c) P1 : — Я не могу назвать числа X и Y.
S1 : — Я заранее знал, что вы не сможете их назвать.
P2 : — Я и после этого не могу назвать числа X и Y.
Требуется отгадать числа X и Y, если их сумма X+Y=11.
1.17) Двое играют в такую игру. В трех клетках записаны числа 1, 2, 3. Начинающий игру должен число в одной клетке заменить целым числом, большим того, которое было записано, но не большим: a) 9, b) 10. Второй игрок делает такой же ход, и так далее. Выигрывает тот, который делает последний ход. Как должен играть первый игрок (начинающий игру), чтобы выиграть при любом ходе второго игрока?
1.18) Найти сумму всех 8! чисел, которые можно получить всевозможными перестановками цифр в числе 12345678.
1.19) a) Двое на счетах играют в такую игру: первый откладывает на счетах любое натуральное число, не большее n, после этого второй добавляет к нему любое натуральное число, не большее n. Затем делает ход первый игрок, и так далее. Выигрывает тот, после хода которого на счетах будет число s,
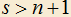. Как должен играть первый игрок, чтобы обеспечить себе победу? Всегда ли это возможно?
b) Двое на счетах играют в такую игру: первый откладывает на счетах любое натуральное число, не большее n, после этого второй добавляет к нему любое натуральное число, не большее n+1. Затем делает ход первый игрок, и так далее. Выигрывает тот, после хода которого на счетах будет число s,
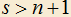. Покажите, что при любой игре первого второй может выиграть игру.
1.20) Восьмикласснику предстоит сдать зачет по математике, на котором ему будет предложено решить 5 задач. Принимать зачет будут две ЭВМ, причем одна из них будет предлагать 3 ответа для каждой задачи, один из которых будет правильный, и эта ЭВМ будет ставить зачет, если ученик решит 3 задачи. Другая будет предлагать два ответа для каждой задачи, один из которых будет правильный, вторая ЭВМ будет ставить зачет, если ученик решит 4 задачи. Какой ЭВМ восьмикласснику выгоднее сдавать зачет? (Выбрать соответствующую ЭВМ нужно до того, как восьмикласснику будут предложены задачи.)
2.1) Решите систему в целых числах:
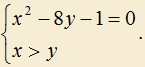
2.2) Решите уравнение в натуральных числах: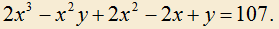
2.3) Докажите, что данное уравнение не разрешимо в целых числах: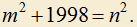
2.4) Решите уравнение относительно a: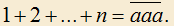
2.5) Решите систему уравнений в натуральных числах: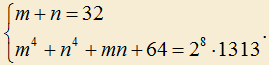
2.6) Решите систему уравнений: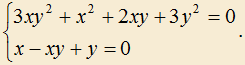
2.7) Доказать неравенство: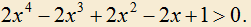
2.8) Решить уравнение: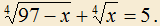
2.9) Решить уравнение: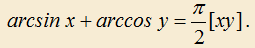
2.10) Решите уравнение: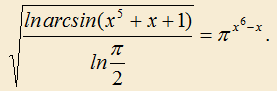
2.11) Найдите все значения параметра a, для которых системы неравенств имеют решения: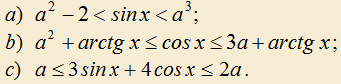
2.12) Найти область определения следующей функции: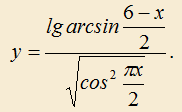
2.13) Доказать, что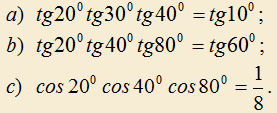
2.14) Решить неравенство: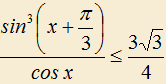
, где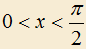 
.
2.15) При каком значении параметра a уравнение имеет единственный корень?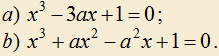
2.16) При каком значении параметра a уравнение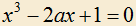
имеет единственный положительный корень?
2.17) При каком значении параметра a>1 уравнение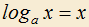
имеет единственное решение?
2.18) Докажите равенство для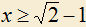
:
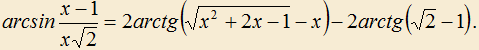
2.19) При каком параметре a>0 система неравенств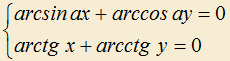
2.20) Девятиклассник Андрей живет в доме D. Каждое утро он ездит в школу на трамвае или на автобусе в направлении, указанном на рисунке. Причем, выходя из дома, Андрей иногда идет на остановку T1, а иногда на остановку T2. Однажды одноклассник Андрея Алексей заинтересовался: случайно ли он выбирает свой маршрут каждое утро?
— Нет, — ответил, Андрей, — не случайно. Когда я выхожу из дома на проезжую часть, я смотрю в направлении моста. Если ожидаемые автобус или трамвай уже пересекли его, то я иду на остановку T1, если же нет, то я иду на остановку T2.
— Но ведь у автобусов и трамваев различные скорости, кроме того, зимой транспорт ходит значительно медленнее. Да и в разное время года ты сам ходишь с разной скоростью — летом быстрее, а весной или осенью — пробираясь через лужи — ты значительно дольше добираешься до остановки.
Андрей улыбнулся.
— Тем не менее, мое правило остается в силе.
Обоснуйте, почему.
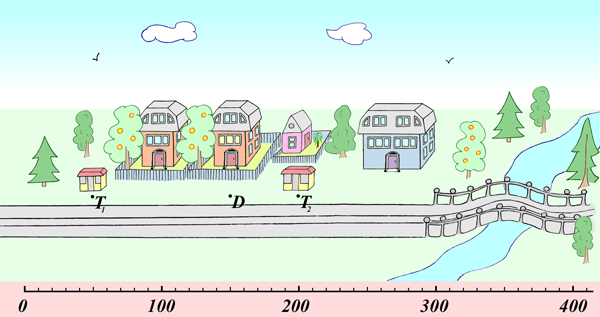
Рис. 1.
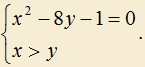
2.2) Решите уравнение в натуральных числах:
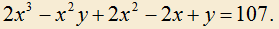
2.3) Докажите, что данное уравнение не разрешимо в целых числах:
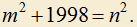
2.4) Решите уравнение относительно a:
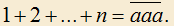
2.5) Решите систему уравнений в натуральных числах:
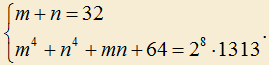
2.6) Решите систему уравнений:
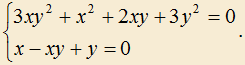
2.7) Доказать неравенство:
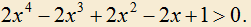
2.8) Решить уравнение:
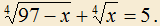
2.9) Решить уравнение:
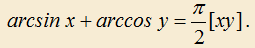
2.10) Решите уравнение:
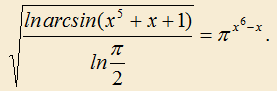
2.11) Найдите все значения параметра a, для которых системы неравенств имеют решения:
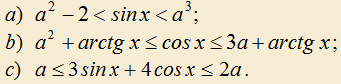
2.12) Найти область определения следующей функции:
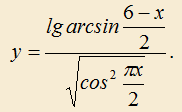
2.13) Доказать, что
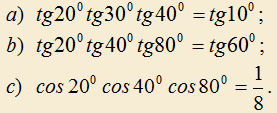
2.14) Решить неравенство:
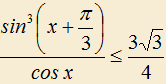, где .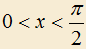
2.15) При каком значении параметра a уравнение имеет единственный корень?
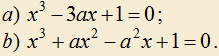
2.16) При каком значении параметра a уравнение
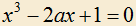имеет единственный положительный корень?
2.17) При каком значении параметра a>1 уравнение
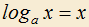имеет единственное решение?
2.18) Докажите равенство для
:
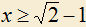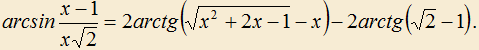
2.19) При каком параметре a>0 система неравенств
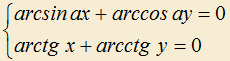
2.20) Девятиклассник Андрей живет в доме D. Каждое утро он ездит в школу на трамвае или на автобусе в направлении, указанном на рисунке. Причем, выходя из дома, Андрей иногда идет на остановку T1, а иногда на остановку T2. Однажды одноклассник Андрея Алексей заинтересовался: случайно ли он выбирает свой маршрут каждое утро?
— Нет, — ответил, Андрей, — не случайно. Когда я выхожу из дома на проезжую часть, я смотрю в направлении моста. Если ожидаемые автобус или трамвай уже пересекли его, то я иду на остановку T1, если же нет, то я иду на остановку T2.
— Но ведь у автобусов и трамваев различные скорости, кроме того, зимой транспорт ходит значительно медленнее. Да и в разное время года ты сам ходишь с разной скоростью — летом быстрее, а весной или осенью — пробираясь через лужи — ты значительно дольше добираешься до остановки.
Андрей улыбнулся.
— Тем не менее, мое правило остается в силе.
Обоснуйте, почему.
3.1) a) Дан параллелограмм ABCD. Прямая, проходящая через вершину B, пересекает диагональ AC в точке Q, а сторону AD в точке P. Найти зависимость между отношениями AP/PD и AQ/QC.
b) На данном отрезке AD=1 построены всевозможные параллелограммы ABCD так, что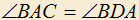 
. Точка P выбрана на AD так, что PD=2PA. Найти ГМТ пересечения отрезков BP и AC.
3.2) В треугольнике ABC проведена биссектриса BD. Доказать, что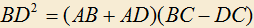
.
3.3) Дан параллелограмм ABCD, AB||CD. Точки E и F выбраны на AD и AB так, что треугольники ABE и ADF подобны. Доказать, что треугольник AME подобен треугольнику CMD, где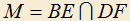
.
3.4) Дана трапеция ABCD, в которой BC||AD, AB=CD. Через точку K внутри трапеции проведены отрезки: MN||AD,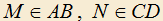
, EK||CN, 
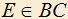, KL||AB, 
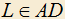. Найти условие, при котором подобны как трапеции MBEK и ABCD, так и образовавшиеся параллелограммы.
3.5) В треугольник ABC вписан треугольник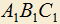
так, что 
, 
, 
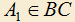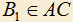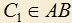, и 
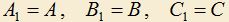(треугольники подобны). Требуется доказать, что окружности, описанные около треугольников 
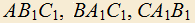равны.
3.6) В параллелограмме ABCD диагонали пропорциональны сторонам: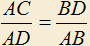
. Доказать, что четыре окружности 
проходят через одну точку, где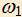 
проходит через вершины A и B и касается BC в точке B, 
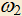проходит через вершины B и C и касается CD в точке C, 
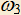проходит через вершины C и D и касается AD в точке D, 
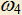проходит через D и A и касается AB в точке A.
3.7) Дан остроугольный треугольник ABC, точка H — точка пересечения его высот. Построены точк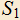и
и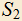 
так, что 
. Докажите, что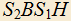 
— параллелограмм, состоящий из двух треугольников, подобных данному треугольнику.
3.8) Дан равнобедренный треугольник ABC, в котором AB=AC ,
. Построен параллелограмм PEBD так, что точка P лежит на AC, точка E — на AB, а точка D — на BC. Построена точка S так, что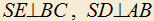 
. Через точку S проведена прямая, SK||AC, 
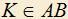. Докажите, что отношение 
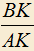не зависит от выбора точки P на AC.
3.9) Из точки A вне окружности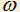
проведены две касательные AP и AQ и перпендикуляр AD на диаметр BC, O — центр 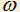. Доказать, что 
.
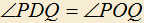3.10) В треугольнике ABC точка H — ортоцентр,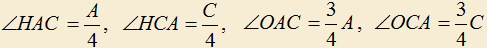
. Доказать, что O — центр описанной окружности.
3.11) В треугольнике ABC построена точка O так, что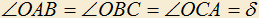
. Обозначим: 
, 
, 
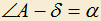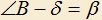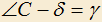. Доказать, что 
.
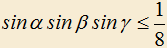3.12) Из точки P на продолжении диаметра AB окружности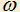
проведена прямая, пересекающая окружность в точках C и D. Построены точки S и H следующим образом: 
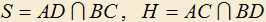. Докажите, что прямая SH — не зависит от выбора секущей CD.
3.13) Дана окружность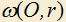
с диаметром AB. Из точки S вне окружности, 
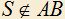, проведены касательные SP и SQ. Стороны SA и SB треугольника SAB пересекают окружность в точках C и D. Доказать, что прямые PQ, CD, AB пересекаются в одной точке.
3.14) Дан угол A величины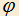
. Построены всевозможные окружности, каждая из которых проходит через вершину A и пересекает стороны угла, причем в таких точках B и C, что AB+AC=s, где s — данный отрезок (данное число). Доказать, что все окружности проходят через одну точку, отличную от A.
3.15) Дан правильный треугольник ABC. Точки E и D выбраны на сторонах AB и AC так, чтобы BE=AD. Точк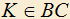и
и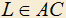 
взяты так, чтобы 
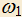и KL||ED. Доказать, что окружности 
и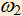 
, описанные около треугольников AED и CKL, касаются, и точка касания — центр треугольника ABC.
3.16) Через две данные точки A и B, AB=2, проведены две окружност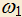и
и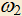 
, центры 
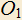и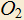 
которых лежат по разные стороны от прямой AB. Построены точк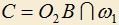и 
и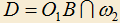 
. Требуется при любом выборе окружности 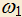выбрать окружность 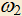так, чтобы точка 
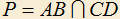была бы постоянной. Как сделать этот выбор? Решить эту задачу при условии, что точк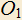и и 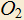лежат по одну сторону от прямой AB.
3.17) В остроугольном треугольнике ABC построены точки: O — центр описанной окружности, J — центр вписанной окружности, H— ортоцентр,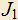
— центр окружности касающейся стороны AC и продолжений сторон BA и BC. Доказать, что
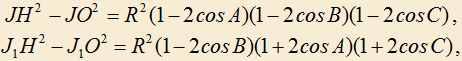
3.18) Даны две скрещивающиеся прямые a и b. Через прямые a и b проведены взаимно перпендикулярные плоскост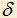и
и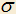 
соответственно, пересекающиеся по прямой MK. Пусть 
, 
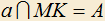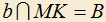. Обозначим острые углы, образованные прямыми a и b с прямой MK через 
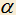и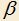 
. Доказать, что произведение 
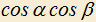не зависит от выбора плоскосте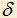й и .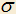
3.19) Дан куб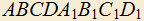
, M — середина ребра AD, N — середина ребра 
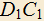. Точка K лежит на BC и BK=2CK. Доказать, что общий перпендикуляр прямых MN и AK лежит вне куба.
3.20) Четыре небольших деревни расположены так, как показано на рисунке. Для того, чтобы снабдить эти деревни питьевой водой необходимо добраться до грунтовых вод, но имеется возможность вырыть только один колодец. Где целесообразнее будет начать строительство такого колодца?
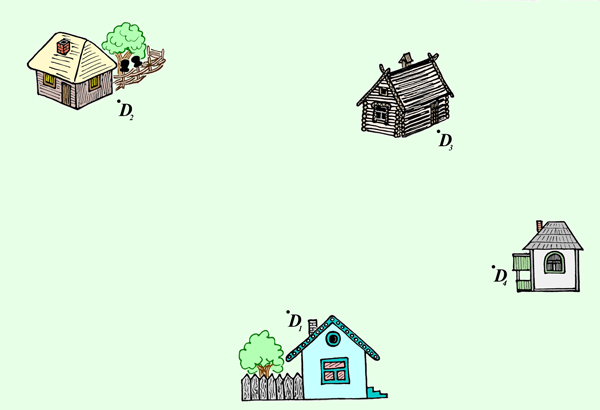
Рис. 2.
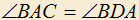. Точка P выбрана на AD так, что PD=2PA. Найти ГМТ пересечения отрезков BP и AC.
3.2) В треугольнике ABC проведена биссектриса BD. Доказать, что
.
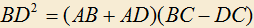3.3) Дан параллелограмм ABCD, AB||CD. Точки E и F выбраны на AD и AB так, что треугольники ABE и ADF подобны. Доказать, что треугольник AME подобен треугольнику CMD, где
.
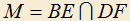3.4) Дана трапеция ABCD, в которой BC||AD, AB=CD. Через точку K внутри трапеции проведены отрезки: MN||AD,
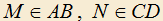, EK||CN, 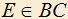, KL||AB, 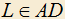. Найти условие, при котором подобны как трапеции MBEK и ABCD, так и образовавшиеся параллелограммы.
3.5) В треугольник ABC вписан треугольник
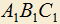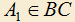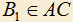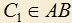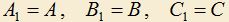так, что , , , и (треугольники подобны). Требуется доказать, что окружности, описанные около треугольников 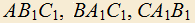равны.
3.6) В параллелограмме ABCD диагонали пропорциональны сторонам:
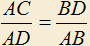. Доказать, что четыре окружности проходят через одну точку, где 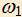проходит через вершины A и B и касается BC в точке B, 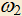проходит через вершины B и C и касается CD в точке C, 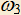проходит через вершины C и D и касается AD в точке D, 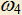проходит через D и A и касается AB в точке A.
3.7) Дан остроугольный треугольник ABC, точка H — точка пересечения его высот. Построены точк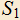и
и 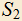так, что . Докажите, что 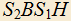— параллелограмм, состоящий из двух треугольников, подобных данному треугольнику.
3.8) Дан равнобедренный треугольник ABC, в котором AB=AC ,
. Построен параллелограмм PEBD так, что точка P лежит на AC, точка E — на AB, а точка D — на BC. Построена точка S так, что 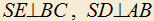. Через точку S проведена прямая, SK||AC, 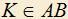. Докажите, что отношение 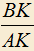не зависит от выбора точки P на AC.
3.9) Из точки A вне окружности
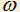проведены две касательные AP и AQ и перпендикуляр AD на диаметр BC, O — центр 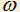. Доказать, что .
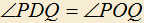3.10) В треугольнике ABC точка H — ортоцентр,
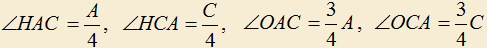. Доказать, что O — центр описанной окружности.
3.11) В треугольнике ABC построена точка O так, что
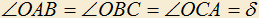. Обозначим: 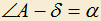, , 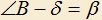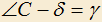. Доказать, что .
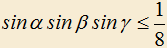3.12) Из точки P на продолжении диаметра AB окружности
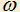проведена прямая, пересекающая окружность в точках C и D. Построены точки S и H следующим образом: 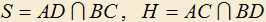. Докажите, что прямая SH — не зависит от выбора секущей CD.
3.13) Дана окружность
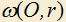с диаметром AB. Из точки S вне окружности, 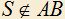, проведены касательные SP и SQ. Стороны SA и SB треугольника SAB пересекают окружность в точках C и D. Доказать, что прямые PQ, CD, AB пересекаются в одной точке.
3.14) Дан угол A величины
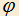. Построены всевозможные окружности, каждая из которых проходит через вершину A и пересекает стороны угла, причем в таких точках B и C, что AB+AC=s, где s — данный отрезок (данное число). Доказать, что все окружности проходят через одну точку, отличную от A.
3.15) Дан правильный треугольник ABC. Точки E и D выбраны на сторонах AB и AC так, чтобы BE=AD. Точк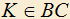и
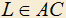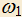и взяты так, чтобы и KL||ED. Доказать, что окружности и 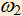, описанные около треугольников AED и CKL, касаются, и точка касания — центр треугольника ABC.
3.16) Через две данные точки A и B, AB=2, проведены две окружност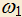и
и 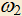, центры 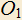и 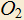которых лежат по разные стороны от прямой AB. Построены точк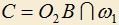и и 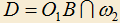. Требуется при любом выборе окружности 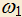выбрать окружность 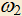так, чтобы точка 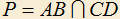была бы постоянной. Как сделать этот выбор? Решить эту задачу при условии, что точк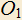и и 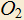лежат по одну сторону от прямой AB.
3.17) В остроугольном треугольнике ABC построены точки: O — центр описанной окружности, J — центр вписанной окружности, H— ортоцентр,
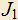— центр окружности касающейся стороны AC и продолжений сторон BA и BC. Доказать, что
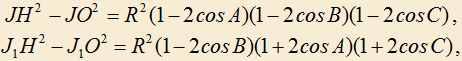
3.18) Даны две скрещивающиеся прямые a и b. Через прямые a и b проведены взаимно перпендикулярные плоскост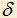и
и 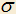соответственно, пересекающиеся по прямой MK. Пусть 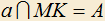, 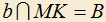. Обозначим острые углы, образованные прямыми a и b с прямой MK через 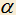и 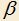. Доказать, что произведение 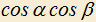не зависит от выбора плоскосте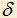й и .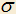
3.19) Дан куб
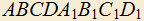, M — середина ребра AD, N — середина ребра 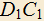. Точка K лежит на BC и BK=2CK. Доказать, что общий перпендикуляр прямых MN и AK лежит вне куба.
3.20) Четыре небольших деревни расположены так, как показано на рисунке. Для того, чтобы снабдить эти деревни питьевой водой необходимо добраться до грунтовых вод, но имеется возможность вырыть только один колодец. Где целесообразнее будет начать строительство такого колодца?
4.1) a) Дан треугольник ABC в котором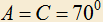 
. Внутри треугольника взята точка M так, что 
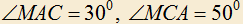. Найти 
.
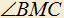b) Дан треугольник ABC в котором
. Внутри треугольника взята точка M так, что 
. Найти .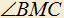
c) Дан треугольник ABC в котором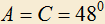
. Внутри треугольника взята точка M так, что 
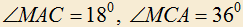. Найти .
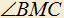4.2) В треугольнике ABC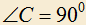
, CJ — биссектриса угла C, 
, 
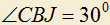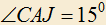. Найти углы A и B.
4.3) Дан треугольник ABC, в котором: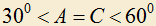
. Точка M внутри треугольника выбрана так, что 
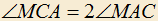и MB=MC. Найти 
.
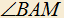4.4) Две окружност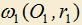и
и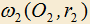 
пересекаются в точках A и B. Касательная к 
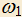в точке B пересекает 
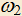в точке D, касательная к 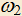в точке B пересекает 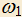в точке C. Известно, что AC=4AD. Найти отношение площадей четырехугольников 
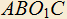и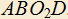 
.
4.5) Дан ромб, который можно разделить на 3 равнобедренных треугольника отрезками, отложенными из одной вершины тупого угла. Найти углы ромба.
4.6) a) В треугольнике ABC проведена биссектриса BD=6. Известно, что AB=2AD, а BC=2DC. Найти стороны треугольника, если известно, что они и отрезки AD и DC выражены целыми числами.
b) Найти все треугольнике ABC в которых все три стороны и биссектриса BD выражены целыми числами и AB+BC=2AC.
4.7) Дан треугольник ABC,
. Требуется внутри треугольника построить точку J так, чтобы 
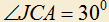и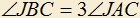 
.
4.8) Дан параллелограмм ABCD с острым углом A. Требуется внутри параллелограмма построить точку M так, чтобы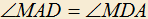
и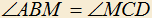 
.
4.9) В данный ромб ABCD,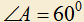
, вписать правильный треугольник DPQ с вершинами P и Q на сторонах AB и BC. При каком выборе точки P на AB сторона треугольника будет наименьшей?
4.10) Вокруг окружности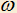
с центром O и радиусом 1 описан треугольник ABC, D — точка касания на стороне AC, отрезок BD пересекает 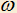в точке E, причем BE=ED. Проведен диаметр DK. Найти:
a) Геометрическое место точек B, если диаметр DK фиксирован.
b) Треугольник ABC с наименьшей площадью и саму эту площадь.
4.11) Даны окружности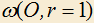
и 
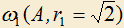, где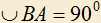 
(рис. 3). Строим треугольник OMK так, что M принадлежит дуге BEC окружности 
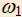, MK — касательная к 
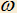, отрезок OM пересекает 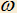в точке D. Требуется определить, при каком выборе точки M на 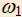площадь треугольника MDK будет наибольшей.
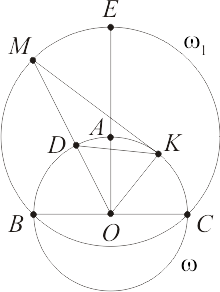
Рис. 3.
4.12) В остроугольном треугольнике ABC проведены высоты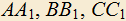
, H — их точка пересечения. Найти все треугольники, в которых отношения 
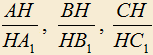выражаются целыми числами.
4.13) В треугольнике ABC точка M обладает тем свойством, что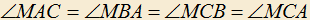
. Найти зависимость между сторонами треугольника и доказать обратное утверждение.
4.14) Через точку A на данной окружности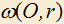
проведена касательная AB и через точку B проведена секущая, пересекающая окружность в точках C и E, точка C лежит между E и B. Прямая, проходящая через точку E и середину M отрезка AB пересекает второй раз окружность в точке K, а прямая BK пересекает второй раз окружность в точке D. При каком выборе секущей BC площадь треугольника ACD будет наибольшей? Зависит ли наибольшая площадь треугольника ACD от длины AB?
4.15) Дан правильный треугольник ABC со стороной 1. Правильный треугольник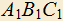
построен так, как показано на рисунке, причем 
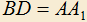. Требуется доказать, что 
. Требуется также выяснить, при каком выборе точки D на AB треугольник 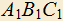будет наименьший.
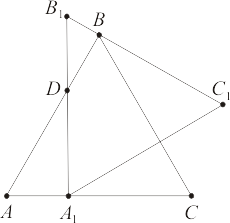
Рис. 4.
4.16) В правильной треугольной пирамиде SABC через середину M высоты SO проведена прямая, пересекающая SA в точке K, а сторону BC в точке D. Найдите отношение KM/MD и объем пирамиды KABC если известно, что объем пирамиды SABC равен 1.
4.17) Через точку M на ребре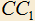
куба 
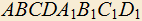проведите прямую, пересекающую прямые AB и 
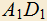. Пусть X и Y — точки пересечения. Требуется найти длину отрезка XY, если ребро куба равно трем, а CM=2. При каком выборе точки M на 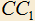длина XY будет наименьшей?
4.18) Дан куб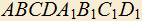
с ребром 1, M — середина ребра 
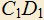, N — середина AB, K — середина BC. Найти расстояние между прямыми AM и NK.
4.19) Дан куб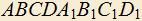
. Построить отрезок наименьшей длины, концы которого лежат на 
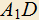и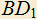 
и который перпендикулярен к прямой 
.
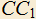4.20) Две деревни расположены по разные стороны от некоторой реки (рис. 5). Необходимо наладить сообщение между этими деревнями, построив мост через реку. Где целесообразнее будет построить такой мост?
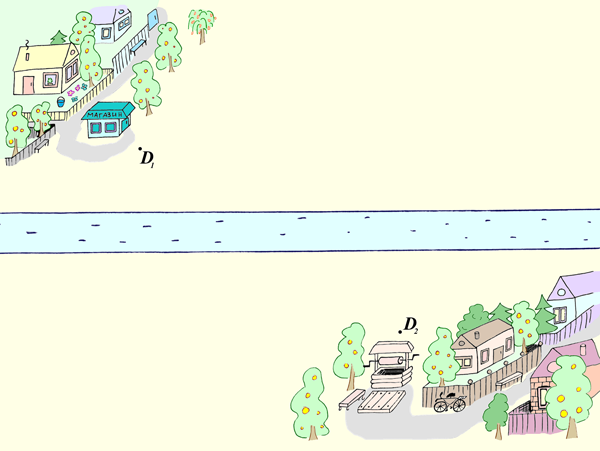
Рис. 5.
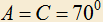. Внутри треугольника взята точка M так, что 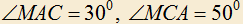. Найти 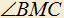.b) Дан треугольник ABC в котором
. Внутри треугольника взята точка M так, что . Найти 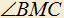.c) Дан треугольник ABC в котором
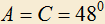. Внутри треугольника взята точка M так, что 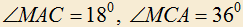. Найти .
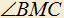4.2) В треугольнике ABC
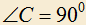, CJ — биссектриса угла C, 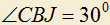, 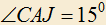. Найти углы A и B.
4.3) Дан треугольник ABC, в котором:
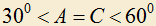. Точка M внутри треугольника выбрана так, что 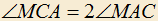и MB=MC. Найти .
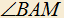4.4) Две окружност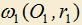и
и 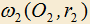пересекаются в точках A и B. Касательная к 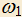в точке B пересекает 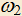в точке D, касательная к 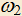в точке B пересекает 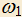в точке C. Известно, что AC=4AD. Найти отношение площадей четырехугольников 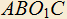и .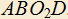
4.5) Дан ромб, который можно разделить на 3 равнобедренных треугольника отрезками, отложенными из одной вершины тупого угла. Найти углы ромба.
4.6) a) В треугольнике ABC проведена биссектриса BD=6. Известно, что AB=2AD, а BC=2DC. Найти стороны треугольника, если известно, что они и отрезки AD и DC выражены целыми числами.
b) Найти все треугольнике ABC в которых все три стороны и биссектриса BD выражены целыми числами и AB+BC=2AC.
4.7) Дан треугольник ABC,
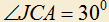. Требуется внутри треугольника построить точку J так, чтобы и .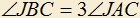
4.8) Дан параллелограмм ABCD с острым углом A. Требуется внутри параллелограмма построить точку M так, чтобы
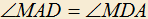и .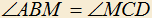
4.9) В данный ромб ABCD,
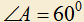, вписать правильный треугольник DPQ с вершинами P и Q на сторонах AB и BC. При каком выборе точки P на AB сторона треугольника будет наименьшей?
4.10) Вокруг окружности
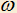с центром O и радиусом 1 описан треугольник ABC, D — точка касания на стороне AC, отрезок BD пересекает 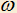в точке E, причем BE=ED. Проведен диаметр DK. Найти:a) Геометрическое место точек B, если диаметр DK фиксирован.
b) Треугольник ABC с наименьшей площадью и саму эту площадь.
4.11) Даны окружности
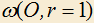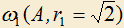и , где 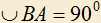(рис. 3). Строим треугольник OMK так, что M принадлежит дуге BEC окружности 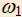, MK — касательная к 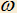, отрезок OM пересекает 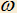в точке D. Требуется определить, при каком выборе точки M на 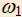площадь треугольника MDK будет наибольшей.
4.12) В остроугольном треугольнике ABC проведены высоты
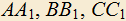, H — их точка пересечения. Найти все треугольники, в которых отношения 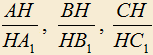выражаются целыми числами.
4.13) В треугольнике ABC точка M обладает тем свойством, что
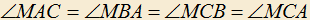. Найти зависимость между сторонами треугольника и доказать обратное утверждение.
4.14) Через точку A на данной окружности
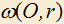проведена касательная AB и через точку B проведена секущая, пересекающая окружность в точках C и E, точка C лежит между E и B. Прямая, проходящая через точку E и середину M отрезка AB пересекает второй раз окружность в точке K, а прямая BK пересекает второй раз окружность в точке D. При каком выборе секущей BC площадь треугольника ACD будет наибольшей? Зависит ли наибольшая площадь треугольника ACD от длины AB?
4.15) Дан правильный треугольник ABC со стороной 1. Правильный треугольник
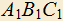построен так, как показано на рисунке, причем 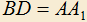. Требуется доказать, что . Требуется также выяснить, при каком выборе точки D на AB треугольник 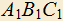будет наименьший.
4.16) В правильной треугольной пирамиде SABC через середину M высоты SO проведена прямая, пересекающая SA в точке K, а сторону BC в точке D. Найдите отношение KM/MD и объем пирамиды KABC если известно, что объем пирамиды SABC равен 1.
4.17) Через точку M на ребре
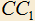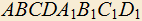куба проведите прямую, пересекающую прямые AB и 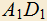. Пусть X и Y — точки пересечения. Требуется найти длину отрезка XY, если ребро куба равно трем, а CM=2. При каком выборе точки M на 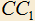длина XY будет наименьшей?
4.18) Дан куб
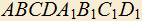с ребром 1, M — середина ребра 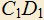, N — середина AB, K — середина BC. Найти расстояние между прямыми AM и NK.
4.19) Дан куб
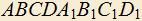. Построить отрезок наименьшей длины, концы которого лежат на 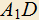и 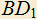и который перпендикулярен к прямой .
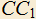4.20) Две деревни расположены по разные стороны от некоторой реки (рис. 5). Необходимо наладить сообщение между этими деревнями, построив мост через реку. Где целесообразнее будет построить такой мост?
5.1) Даны три простых числа: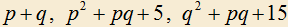 
, где p и q — некоторые натуральные числа. Найти p и q.
5.2) Доказать, что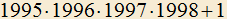
есть полный квадрат.
5.3) Про натуральные числа a, b, c, m, n, k известно, что a+b+c=m+n+k=24, и a(m+n)=k(b+c). Найти наибольшее значение для a(m+n).
5.4) Докажите, что для любых натуральных n и k
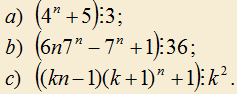
5.5) Могут ли три последовательных члена арифметической прогрессии с разностью, отличной от нуля, быть одновременно последовательными членами геометрической прогрессии?
5.6) Три простых числа, большие 3, образуют арифметическую прогрессию. Доказать, что разность прогрессии делится на 6.
5.7) Три натуральных числа составляют геометрическую прогрессию со знаменателем, отличным от единицы. Найти эти числа, если их сумма a) 129; b) 91.
5.8) Доказать, что если положительные числа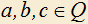
удовлетворяют равенству 
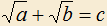, то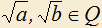 
.
5.9) Найти все натуральные числа, которые при делении на 5 являются квадратами, а при делении на 2 — кубами натуральных чисел.
5.10) Какое время покажут часы, если часовая стрелка будет находиться между одиннадцатью и двенадцатью, и с минутной стрелкой будет образовывать развернутый угол?
5.11) Угол между Солнцем, Луной и наблюдателем, находящемся на Земле, составляет 120 градусов. Луна представляется наблюдателю в виде Месяца. Найти отношение площади этого Месяца (как плоской фигуры) к площади диска Луны, который нам представляется в виде круга. Найти также отношение площади лунной поверхности, освещенной Солнцем и видимой наблюдателю, к площади всей поверхности Луны.
5.12) Даны две скрещивающиеся прямые (рис. 6), расстояние между которыми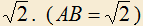
. Точки A и B одновременно начинают двигаться вдоль этих прямых равномерно со скоростью v=1. Когда расстояние между точками становится равным 
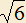, одна из них меняет направление движения на противоположное, и когда она возвращается в исходное положение, расстояние между ними становится 
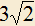. Точка, не останавливаясь, продолжает движение. Через какое время после этого расстояние между точками станет 
?
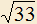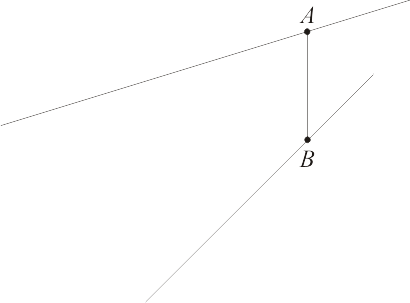
Рис. 6.
5.13) Дан остроугольный треугольник ABC, в котором проведены высоты BD и CE. Точка B передвигается равномерно по высоте BD, а точка C — по высоте CE. Известно, что они встретятся в точке H пересечения высот. Если точка B будет передвигаться по стороне BA, а точка C по стороне CA с прежними скоростями, то какая точка первой прибудет в точку A, если известно, что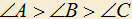
?
5.14) Упростите:
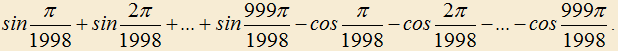
5.15) Выберем подпоследовательность натурального ряда так, чтобы первым ее членом была 1, а каждый последующий член находился по формуле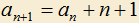
. Выведите формулу n-го члена данной подпоследовательности.
5.16) Какие значения может принимать a, есл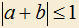и
и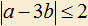 
?
5.17) Два тела движутся равномерно по окружности в одну сторону. Первое тело проходит окружность на 3 секунды быстрее второго, и догоняет второе тело каждые полторы минуты. За какое время каждое тело проходит окружность?
5.18) Разложите на множители сумму:
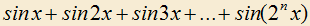
5.19) Найти f(t), если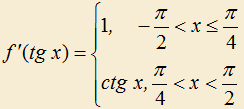
и f(0)=1.
5.20) В одной из сельских больниц срочно требуется перелить кровь человеку, попавшему в автомобильную катастрофу. Но в больнице нет банка крови и нет реактивов для определения группы крови. И тогда врач решается на то, чтобы перелить кровь пациенту от первого желающего донора, ибо безнадежность ситуации не оставляет выбора. Какова вероятность того, что такой отчаянный поступок не приведет к печальным последствиям?
Известно, что процентное соотношение людей с соответствующими группами крови (I, II, III и IV) составляет 46%, 42%, 9% и 3%. Известно также, что около 85% людей обладают положительным резус-фактором, и около 15% — отрицательным. Для корректности задачи будем считать, что никто из описанного села не знает свою группу крови. (В данной задаче понадобятся знания основ медицины.)
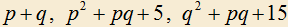, где p и q — некоторые натуральные числа. Найти p и q.
5.2) Доказать, что
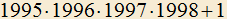есть полный квадрат.
5.3) Про натуральные числа a, b, c, m, n, k известно, что a+b+c=m+n+k=24, и a(m+n)=k(b+c). Найти наибольшее значение для a(m+n).
5.4) Докажите, что для любых натуральных n и k
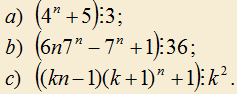
5.5) Могут ли три последовательных члена арифметической прогрессии с разностью, отличной от нуля, быть одновременно последовательными членами геометрической прогрессии?
5.6) Три простых числа, большие 3, образуют арифметическую прогрессию. Доказать, что разность прогрессии делится на 6.
5.7) Три натуральных числа составляют геометрическую прогрессию со знаменателем, отличным от единицы. Найти эти числа, если их сумма a) 129; b) 91.
5.8) Доказать, что если положительные числа
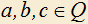удовлетворяют равенству 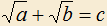, то .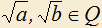
5.9) Найти все натуральные числа, которые при делении на 5 являются квадратами, а при делении на 2 — кубами натуральных чисел.
5.10) Какое время покажут часы, если часовая стрелка будет находиться между одиннадцатью и двенадцатью, и с минутной стрелкой будет образовывать развернутый угол?
5.11) Угол между Солнцем, Луной и наблюдателем, находящемся на Земле, составляет 120 градусов. Луна представляется наблюдателю в виде Месяца. Найти отношение площади этого Месяца (как плоской фигуры) к площади диска Луны, который нам представляется в виде круга. Найти также отношение площади лунной поверхности, освещенной Солнцем и видимой наблюдателю, к площади всей поверхности Луны.
5.12) Даны две скрещивающиеся прямые (рис. 6), расстояние между которыми
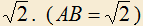. Точки A и B одновременно начинают двигаться вдоль этих прямых равномерно со скоростью v=1. Когда расстояние между точками становится равным 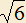, одна из них меняет направление движения на противоположное, и когда она возвращается в исходное положение, расстояние между ними становится 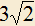. Точка, не останавливаясь, продолжает движение. Через какое время после этого расстояние между точками станет ?
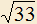5.13) Дан остроугольный треугольник ABC, в котором проведены высоты BD и CE. Точка B передвигается равномерно по высоте BD, а точка C — по высоте CE. Известно, что они встретятся в точке H пересечения высот. Если точка B будет передвигаться по стороне BA, а точка C по стороне CA с прежними скоростями, то какая точка первой прибудет в точку A, если известно, что
?
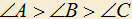5.14) Упростите:
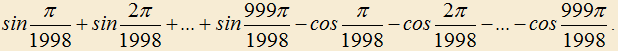
5.15) Выберем подпоследовательность натурального ряда так, чтобы первым ее членом была 1, а каждый последующий член находился по формуле
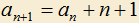. Выведите формулу n-го члена данной подпоследовательности.
5.16) Какие значения может принимать a, есл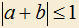и
и ?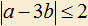
5.17) Два тела движутся равномерно по окружности в одну сторону. Первое тело проходит окружность на 3 секунды быстрее второго, и догоняет второе тело каждые полторы минуты. За какое время каждое тело проходит окружность?
5.18) Разложите на множители сумму:
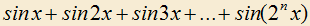
5.19) Найти f(t), если
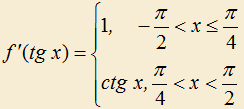и f(0)=1.
5.20) В одной из сельских больниц срочно требуется перелить кровь человеку, попавшему в автомобильную катастрофу. Но в больнице нет банка крови и нет реактивов для определения группы крови. И тогда врач решается на то, чтобы перелить кровь пациенту от первого желающего донора, ибо безнадежность ситуации не оставляет выбора. Какова вероятность того, что такой отчаянный поступок не приведет к печальным последствиям?
Известно, что процентное соотношение людей с соответствующими группами крови (I, II, III и IV) составляет 46%, 42%, 9% и 3%. Известно также, что около 85% людей обладают положительным резус-фактором, и около 15% — отрицательным. Для корректности задачи будем считать, что никто из описанного села не знает свою группу крови. (В данной задаче понадобятся знания основ медицины.)